みなさん、ティープラーニングで (株価|為替) やってますでしょうか?私は先月は今まで書いていなかったテストを書き、今月は他の出費が多すぎて GPU を回す余裕が無いため進捗はほぼありません本当にありがとうございました。
さて今回はディープラーニングでの株価予測についてです。ディープラーニングで株価を予測しようとする際に真っ先に思いつくモデルが LSTM です。LSTM は時系列データの処理に向いており、なんと偶然にも株価データも時系列データなのでこれを使えば上手く株価を予測できるのではないかと思うのは当然といえば当然です。しかし、実際やってみると上手く行かないことがほとんどだと思います。そこで、上手く行かないパターンのうちの 1 つを考察していきます。
使用するデータ
http://k-db.com/indices/I101 の日経平均株価 2007 年 〜 2017 年の日足データを使います。
ディープラーニングで株価予測
モデルは 10 日分の日経平均株価を入力として、1 日後の日経平均株価を予測することとします。ですので、取得したデータを読み込んで日付順にソートした後、終値だけを取り出します。
def read_data():
paths = Path('.').glob('./indices_I101_1d_*.csv')
df = pd.concat([pd.read_csv(p, index_col='日付', parse_dates=True, encoding='cp932')
for p in paths])
df = df.sort_index()
closes = df['終値'].values
return closes
今回のネットワークはごく単純な LSTM とし、Keras を使って組んでいきます。
def create_model():
inputs = Input(shape=(10, 1))
x = LSTM(300, activation='relu')(inputs)
price = Dense(1, activation='linear', name='price')(x)
updown = Dense(1, activation='sigmoid', name='updown')(x)
model = Model(inputs=inputs, outputs=[price, updown])
model.compile(loss={
'price': 'mape',
'updown': 'binary_crossentropy',
}, optimizer='adam', metrics={'updown': 'accuracy'})
return model
日経平均株価の値を直接予測するため活性化関数は linear を使います。中間層の数は 300 としていますが特に理由はありません。後で検証に使用するため 2 値予測も含んでいます。
全データのうち、80% を学習用データ、20% を検証用データに割り当てます。また、データの標準化も行います。
def build_train_test_data(base_data):
scaler = StandardScaler()
data = scaler.fit_transform(base_data)
x_data = []
y_data_price = []
y_data_updown = []
for i in range(len(data) - 10):
x_data.append(data[i:i + 10])
y_data_price.append(data[i + 10])
y_data_updown.append(int((base_data[i + 10 - 1] - base_data[i + 10]) > 0))
x_data = np.asarray(x_data).reshape((-1, 10, 1))
y_data_price = np.asarray(y_data_price)
y_data_updown = np.asarray(y_data_updown)
train_size = int(len(data) * 0.8)
x_train = x_data[:train_size]
y_train_price = y_data_price[:train_size]
y_train_updown = y_data_updown[:train_size]
x_test = x_data[train_size:]
y_test_price = y_data_price[train_size:]
y_test_updown = y_data_updown[train_size:]
return x_train, y_train_price, y_train_updown, x_test, y_test_price, y_test_updown, scaler
では学習していきます。エポックは 100、バッチサイズは 10 としていますが、これらも特に理由はありません。
def main():
model = create_model()
data = read_data()
x_train, y_train_price, y_train_updown, x_test, y_test_price, y_test_updown, scaler = \
build_train_test_data(data)
model.fit(x_train, [y_train_price, y_train_updown],
validation_data=(x_test, [y_test_price, y_test_updown]), epochs=100, batch_size=10,
callbacks=[CSVLogger('train.log.csv')])
model.save('model.h5')
with open('scaler.pkl', 'wb') as f:
pickle.dump(scaler, f, protocol=pickle.HIGHEST_PROTOCOL)
pred = model.predict(x_test)[0][:, 0].reshape(-1)
pred = scaler.inverse_transform(pred)
y_test_price = scaler.inverse_transform(y_test_price.astype('float64'))
result = pd.DataFrame({'pred': pred, 'test': y_test_price})
result.plot()
plt.show()
Fig. 1 は学習したモデルで予測した日経平均株価のグラフです。
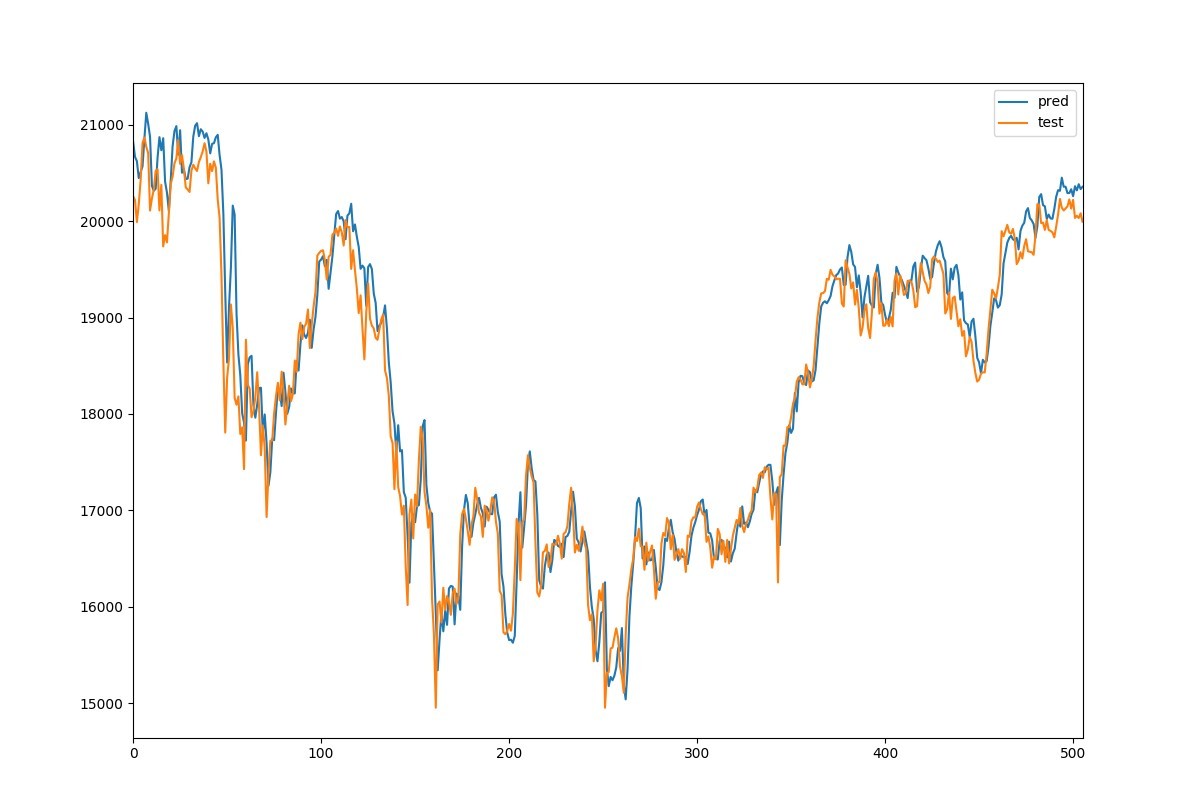
縦軸が株価で横軸が日数、青の線が予測した株価、オレンジの線が実際の株価です。これを見るとなかなか良さそうに見えます。本当でしょうか?もう少し細かく見れるように拡大してみます。
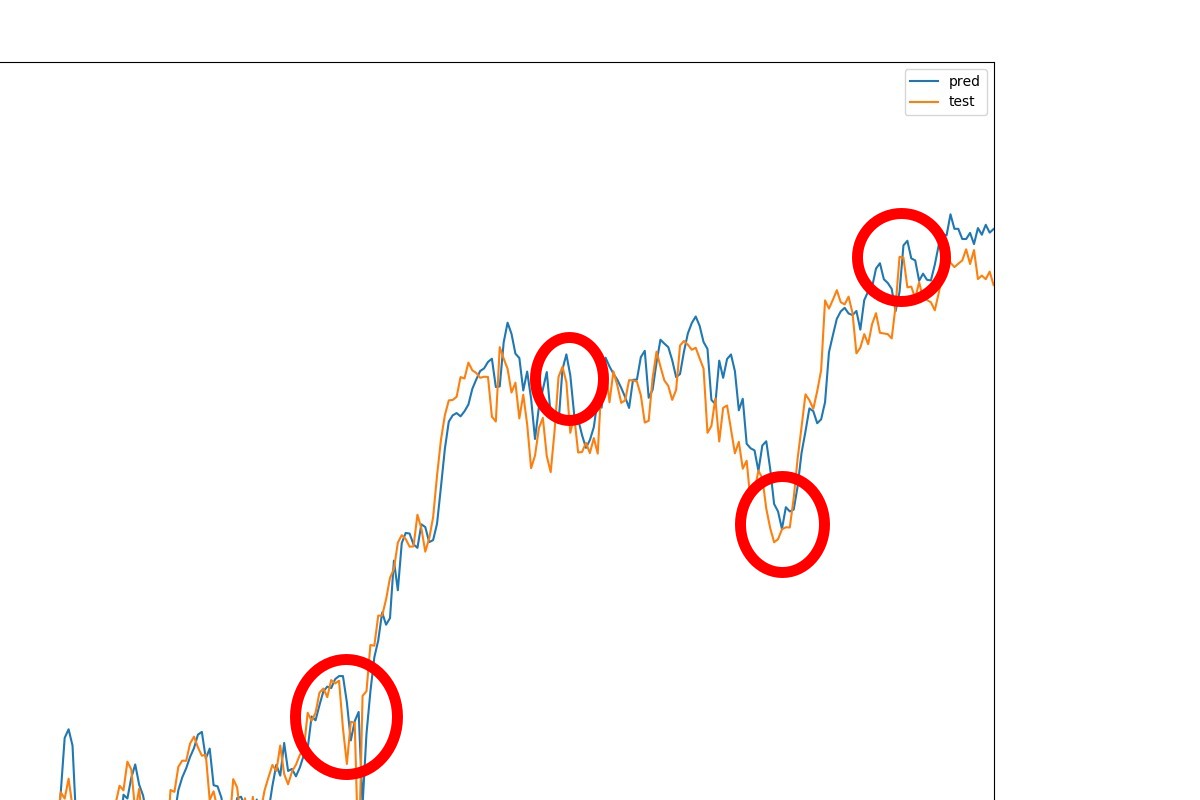
これを見ると、実際の株価の線より予測した株価の線が右側にあります。つまり、実際の株価を見てから同じような株価を予測していると考えられます。とすると、このモデルが行っているのは後出しジャンケンであり、実際には回帰の予測精度は良くないはずです。
回帰の予測精度の検証
回帰が上手くいっているのであれば同様に分類の精度も良いはずと仮定します。なぜならば、回帰による予測値が現在の株価より上 (下) の株価の場合は分類において上がる (下がる) と予測しているとみなすことができるためです。この仮定を前提にして、回帰のときと同様のモデルを用いて 2 値分類 (明日の株価は上がるか下がるか) の精度を出すことによって回帰の精度の良し悪しを判定します。2 値分類の精度が高ければ同じように回帰の精度も高く、逆に 2 値分類の精度が低ければ回帰の精度も低いとみなします。
では学習時のログを見てみましょう。
Epoch 91/100
2060/2060 [==============================] - 6s - loss: 28.7736 - price_loss: 28.0817 - updown_loss: 0.6919 - updown_acc: 0.5209 - val_loss: 6.7649 - val_price_loss: 6.0684 - val_updown_loss: 0.6965 - val_updown_acc: 0.5217
Epoch 92/100
2060/2060 [==============================] - 6s - loss: 24.3430 - price_loss: 23.6510 - updown_loss: 0.6920 - updown_acc: 0.5199 - val_loss: 6.5385 - val_price_loss: 5.8425 - val_updown_loss: 0.6961 - val_updown_acc: 0.5217
Epoch 93/100
2060/2060 [==============================] - 6s - loss: 26.3017 - price_loss: 25.6097 - updown_loss: 0.6920 - updown_acc: 0.5194 - val_loss: 6.4435 - val_price_loss: 5.7476 - val_updown_loss: 0.6959 - val_updown_acc: 0.5217
Epoch 94/100
2060/2060 [==============================] - 6s - loss: 27.6540 - price_loss: 26.9620 - updown_loss: 0.6921 - updown_acc: 0.5209 - val_loss: 5.9723 - val_price_loss: 5.2771 - val_updown_loss: 0.6953 - val_updown_acc: 0.5217
Epoch 95/100
2060/2060 [==============================] - 6s - loss: 20.9458 - price_loss: 20.2539 - updown_loss: 0.6919 - updown_acc: 0.5218 - val_loss: 6.7548 - val_price_loss: 6.0571 - val_updown_loss: 0.6977 - val_updown_acc: 0.5217
Epoch 96/100
2060/2060 [==============================] - 6s - loss: 26.4059 - price_loss: 25.7140 - updown_loss: 0.6919 - updown_acc: 0.5199 - val_loss: 6.3378 - val_price_loss: 5.6411 - val_updown_loss: 0.6967 - val_updown_acc: 0.5217
Epoch 97/100
2060/2060 [==============================] - 6s - loss: 25.6863 - price_loss: 24.9944 - updown_loss: 0.6919 - updown_acc: 0.5209 - val_loss: 6.3354 - val_price_loss: 5.6380 - val_updown_loss: 0.6975 - val_updown_acc: 0.5217
Epoch 98/100
2060/2060 [==============================] - 6s - loss: 24.8471 - price_loss: 24.1552 - updown_loss: 0.6919 - updown_acc: 0.5214 - val_loss: 6.1885 - val_price_loss: 5.4909 - val_updown_loss: 0.6976 - val_updown_acc: 0.5217
Epoch 99/100
2060/2060 [==============================] - 6s - loss: 29.4966 - price_loss: 28.8046 - updown_loss: 0.6920 - updown_acc: 0.5238 - val_loss: 10.1860 - val_price_loss: 9.4882 - val_updown_loss: 0.6977 - val_updown_acc: 0.5217
Epoch 100/100
2060/2060 [==============================] - 6s - loss: 23.0722 - price_loss: 22.3801 - updown_loss: 0.6921 - updown_acc: 0.5204 - val_loss: 6.5638 - val_price_loss: 5.8681 - val_updown_loss: 0.6957 - val_updown_acc: 0.5217
updown_acc (学習用データでの精度)、val_updown_acc (検証用データでの精度) のどちらも 52% 程度となっています。単純に考えると上がるか下がるかが当たる確率は 50% なので、52% という予測精度は 2 値予測においては高い精度とは言えません。そのため、仮定より、同様に回帰の精度も高い精度とは言えないことになります。
学習したモデルを使った売買シミュレーション
学習したモデルを使った 2007 年 1 月から 2017 年 7 月までの日経平均株価の売買シミュレーションの結果を Fig. 3 に示します。
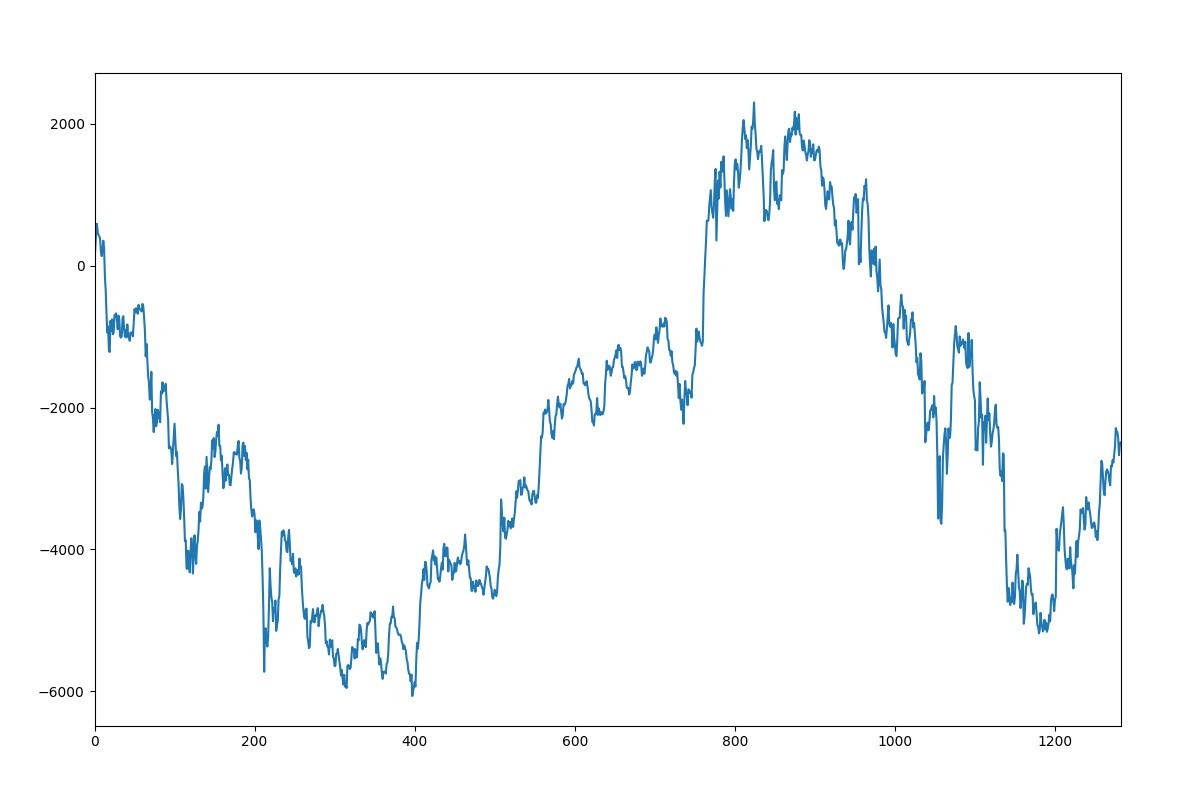
シミュレーションはレバレッジ無しの 1 単位で行い、縦軸が利益 (単位: 円)、横軸がポジションを取った数です。見ての通り大きく乱高下して安定しておらず、最終的にマイナスになっています。この結果から見ても、今回のモデルの精度は高くないことが伺えます。
まとめ
ディープラーニングをやっていると、一見良さそうな結果に見えてもよくよく考えたり検証したりすると実は・・・ということが稀によくあります。ほとんどはデータセットの間違いや、学習用データに正解ラベルが混じってるのが原因ですが、そうでなくてもこういったことがあったりします 1 ので、ディープラーニングで (株価|為替) 予測各位は頑張っていきましょう (自戒)。
今回使用した全コード
import pickle
from pathlib import Path
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from keras.layers import Input, Dense, LSTM
from keras.models import Model
from keras.callbacks import CSVLogger
from sklearn.preprocessing import StandardScaler
def read_data():
paths = Path('.').glob('./indices_I101_1d_*.csv')
df = pd.concat([pd.read_csv(p, index_col='日付', parse_dates=True, encoding='cp932')
for p in paths])
df = df.sort_index()
closes = df['終値'].values
return closes
def create_model():
inputs = Input(shape=(10, 1))
x = LSTM(300, activation='relu')(inputs)
price = Dense(1, activation='linear', name='price')(x)
updown = Dense(1, activation='sigmoid', name='updown')(x)
model = Model(inputs=inputs, outputs=[price, updown])
model.compile(loss={
'price': 'mape',
'updown': 'binary_crossentropy',
}, optimizer='adam', metrics={'updown': 'accuracy'})
return model
def build_train_test_data(base_data):
scaler = StandardScaler()
data = scaler.fit_transform(base_data)
x_data = []
y_data_price = []
y_data_updown = []
for i in range(len(data) - 10):
x_data.append(data[i:i + 10])
y_data_price.append(data[i + 10])
y_data_updown.append(int((base_data[i + 10 - 1] - base_data[i + 10]) > 0))
x_data = np.asarray(x_data).reshape((-1, 10, 1))
y_data_price = np.asarray(y_data_price)
y_data_updown = np.asarray(y_data_updown)
train_size = int(len(data) * 0.8)
x_train = x_data[:train_size]
y_train_price = y_data_price[:train_size]
y_train_updown = y_data_updown[:train_size]
x_test = x_data[train_size:]
y_test_price = y_data_price[train_size:]
y_test_updown = y_data_updown[train_size:]
return x_train, y_train_price, y_train_updown, x_test, y_test_price, y_test_updown, scaler
def main():
model = create_model()
data = read_data()
x_train, y_train_price, y_train_updown, x_test, y_test_price, y_test_updown, scaler = \
build_train_test_data(data)
model.fit(x_train, [y_train_price, y_train_updown],
validation_data=(x_test, [y_test_price, y_test_updown]), epochs=100, batch_size=10,
callbacks=[CSVLogger('train.log.csv')])
model.save('model.h5')
with open('scaler.pkl', 'wb') as f:
pickle.dump(scaler, f, protocol=pickle.HIGHEST_PROTOCOL)
pred = model.predict(x_test)[0][:, 0].reshape(-1)
pred = scaler.inverse_transform(pred)
y_test_price = scaler.inverse_transform(y_test_price.astype('float64'))
result = pd.DataFrame({'pred': pred, 'test': y_test_price})
result.plot()
plt.show()
if __name__ == '__main__':
main()
-
当然今回の仮説と検証が間違っている可能性もありますが。 ↩︎